Diversification

Unique Risk Series – Article 1 out of 3

– Diversification
– Minimum Variance Portfolio
– Market Portfolio

---

The stock market is a wild, crazy, and sometimes scary place. Especially these days with the extreme volatility of the past few years and the recurring news of corrupt bankers and their devious practices.

But the stock market, whether we like it or not, is one of the best places to build wealth.

To reap the benefits of the market, do you have to simply accept the fact that you need to just dive in and become a bobbing ship in a large, violent, and unpredictable ocean?

Not exactly.

There are aspects of investing in the stock market that are within your control that can greatly affect your total returns. So instead of focusing on the things that you can’t control, focus on the things that you can.

The first aspect of investing that you can control, which I am going to discuss in this article series, is unique risk.

There is quite a bit of background information that I need to supply to properly describe how to eliminate unique risk so I’m going to break this topic into three separate, action-packed articles.

So get comfortable and get a nicely sharpened #2 pencil ready because we are about to geek out with some math and financial theory!

Unique Risk

Your portfolio’s risk is made up of two parts: Market (Systemic) Risk and Unique (Idiosyncratic) Risk.

Total Risk = Unique Risk + Market Risk

Market risk represents economy-wide factors that are out of your control, like interest rates, government spending, inflation, etc.

Unique risk represents firm-specific factors such as labor strikes, patent decisions, competitor emergence, etc.

There is not much you can do about market risk so if you want to invest in the market, you have to accept that you will be exposed to market risk.

Unique risk, however, is within your control. If you understand unique risk and take it into account when building your portfolio, you can greatly reduce the amount of overall risk your portfolio is exposed to.

So how can you eliminate unique risk?

Diversification.

As you combine different types of stocks in your portfolio, you begin to decrease the amount of unique risk you are exposed to. If you have many different types of stocks in your portfolio, unique risk ceases to be a factor at all and you are left with only market risk.

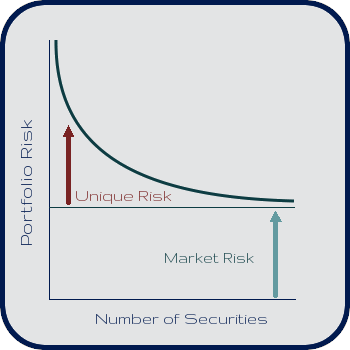
Scenario

Say you invest in Stock A. Stock A is a nice, stable “blue-chip” company stock that isn’t too exciting but isn’t too scary either. It hasn’t been very volatile in the past but it hasn’t exactly tripled in value every year either. You are happy with this stock and are comfortable with the risk associated with owning it.

Being a fientist who loves technology, you discover a company that you know is going to do great things, you just don’t know when. The company’s stock, however, is very volatile and sees major daily swings. You want to invest in Stock B but you don’t think your stomach can take it.

Someone who does not know how diversification works would probably assume that adding Stock B to your portfolio would always increase the risk of the portfolio. In actuality, it is possible that adding Stock B could lower your portfolio’s risk!

How could adding a riskier stock to a less risky stock make the combination of the two less risky than even the less risky stock on its own? It’s all about how the stocks are correlated with each other. Here comes that sexy mathematics that I promised you earlier…

Mmm, math

Variance is the unit of measure for risk (standard deviation, which is simply the square root of the variance value, is also a measure of risk).

When building a portfolio, you want to try to do one of two things (preferably both): lower the variance and/or increase the expected return.

In other words, you want to make more money while having less stress.

So say Stock A has an expected return of 4% and a standard deviation of 6% and Stock B has an expected return of 8% and a standard deviation of 15%. You’d expect that by combining the two stocks in your portfolio, your portfolio’s expected return and standard deviation would be an average of the two individual values. While that is true for the expected return value, it’s not the case for the standard deviation.

When combining two stocks, you must determine their correlation with each other to understand how much risk the combination of the stocks produces. If the two stocks mentioned above are negatively correlated with each other, adding the riskier stock to the portfolio can actually lower your portfolio’s risk!

The equations for expected return and portfolio variance for a two-asset portfolio are:

Expected Return = (x_ar_a) + (x_br_b)

x_a = Percentage invested in Stock A
r_a = Expected return of Stock A
x_b = Percentage invested in Stock B
r_b = Expected return of Stock B

Portfolio Variance = x_a²σ_a² + x_b²σ_b² + 2(x_ax_bρ_abσ_aσ_b)

x_a = Percentage invested in Stock A
x_b = Percentage invested in Stock B
σ_a = Standard deviation of Stock A
σ_b = Standard deviation of Stock B
ρ_ab = Correlation between Stocks A and B

So in this example, the expected return of a portfolio consisting of an equal amount of Stock A and Stock B would be:

Expected Return = (0.50 * 4) + (0.50 * 8) = 6%

As expected, the expected return of the portfolio is the average of the expected returns of the individual stocks.

If the two stocks are negatively correlated (let ρ_ab = -0.70), the variance of the two-stock portfolio is:

Portfolio Variance = (0.50² * 6²) + (0.50² * 15²) + (2 * 0.50 * 0.50 * -0.70 * 6 * 15) = 33.75

Using the variance value of 33.75, we can easily compute the portfolio’s standard deviation by taking the square root:

Portfolio Standard Deviation = √33.75 = 5.81%

In this example, adding Stock B to your portfolio is a great idea because it should increase your expected return from 4% to 6% while also lowering your portfolio’s standard deviation from 6% to 5.81%!

Conclusion

As we’ve just seen, an individual stock’s riskiness doesn’t matter; it is the correlation between the individual stock and your existing portfolio and how the individual stock affects the portfolio’s risk that actually determines whether a stock would be a good investment.

So does this mean you should go out and start picking a bunch of individual stocks to invest in? Not necessarily.

Next time I will discuss the minimum variance portfolio and will describe how to best construct a portfolio that minimizes unique risk.

Next article in the Unique Risk series: Minimum Variance Portfolio