Should you pay off your mortgage early or invest?
I get this question a lot (twice in the last week, actually).
One year ago, a reader named Clay bought a new house and had to make this exact decision.
Note: You may remember Clay from this 2015 post – Financial Independence After Tragedy
Lucky for us, he decided to do a bit of both and he’s tracked all his numbers to compare the two options!
Clay doesn’t have his own blog so he kindly reached out to me to share his findings.
Obviously your investment returns will differ and you can’t predict what the markets are going to do in any given year but it’s interesting to see how the numbers in this real-life experiment are playing out.
Take it away, Clay…
You’ve read all the articles and heard all the debates.
The “All Debt Is Evil” camp declares…
“Payoff the mortgage as fast as possible! Your damn hair is on FIRE! Debt is the spawn of SATAN! Once the house is paid off you will have enormous cash flow! Pay it off! PAY IT OFF!!!!”
The “Smarter Than Thou” finance ninja will tell you…
“Mortgages are GOOD DEBT! Investments are the way to go. Borrow at 4% and earn 7% in the market! It is simple math you moron. Plus tax law is in your favor. Don’t put your money in the house…put it in investments.”
The decision between mortgage payoff and investing is really about balancing the psychology of living debt free with your own personal risk tolerance (with an extra side dish of finance efficiency).
This past year I found myself in a situation where I could run an actual test, with actual money, on my actual house.
Last year my wife and I bought a house for our newly blended family. When my old house sold, we had enough cash to pay off our new mortgage.
So I had a few choices…
OPTION (1) Pay off that mortgage, burn that bank statement, and invest that extra cash each month. Dave Ramsey would be proud.
OPTION (2) Keep my newly minted 30-yr mortgage and stick the funds from the old place in 100% stocks and watch CNBC for hours each night since I will no longer be able to sleep.
What to do, what to do?
How about a compromise that gives a sense of security and still leaves funds in the market? Wouldn’t that be sweet? Isn’t all personal finance personal? So why not do a little of both?
Step one, pay off a portion of the mortgage to bring it down to $200k. This is a nice round number and the reduction of principal shrinks the 30-year term to just over 16 years. Now, I’m paying more in principal than interest each month AND I have a bunch of equity in the house. All this makes me feel better. MATH BE DAMNED!
Step two, take that same nice $200k round number and invest it.
Where should it go? VTSAX? Yeah, maybe I would do that if it were the Mad Fientist’s money but this is my own scratch we’re talking about here. This is not just theory, I am actually doing this. So a nice blended fund that generates income would be perfect. I want to have the income from this fund go directly into my checking account instead of being reinvested, because hey, I am sort of semi-retired at this point and care about having some income. Plus there are these things called mortgage payments I still need to make.
I ended up landing on the Vanguard Wellesley Income Fund Admiral Shares (VWIAX), which is an income-based balanced fund.
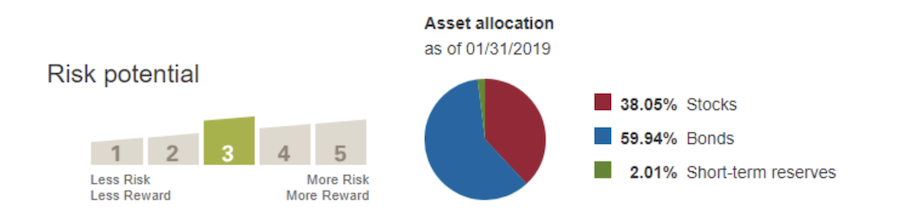
Yes I could have gone more aggressive and yes I could have re-invested the distributions but hey…this ain’t no disco…this ain’t no foolin’ around. I still need to make sure that my wife and I can sleep at night and the combination of regular income in a balanced fund gives me the confidence that I’m still putting my greenback soldiers to work in a responsible way.
So here we go…
As of June 2018, there are now two competing line items in my spreadsheet:
Investment
$200k into VWIAX fund (3,148.119 shares @ $63.53).
This has a historic market gain of 6.8% according to Vanguard and pays quarterly dividends.
The value will change with the market.
Mortgage
$200k at 3.99% with term of 16 years 8 months.
Monthly P+I is $1368.53. The amount owed steadily goes down as it is paid off.
Results
How do we compare?
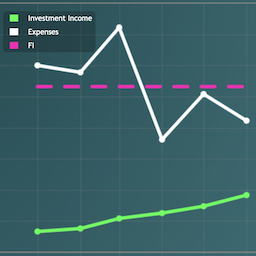
Unlike watching two racers who would deftly maneuver and muscle for rank, trying to compare paying off a mortgage to a stock fund in real-time isn’t as easy as you’d think.
Compare the Balances
Don’t you just compare the fund balance vs. mortgage balance? Duh. What could be simpler?
Every month, the mortgage shrinks and the fund bounces up and down with the market. I can just compare the balance between the two. If I subtract them I get what I call the “What if I just pay off the mortgage?” graph.
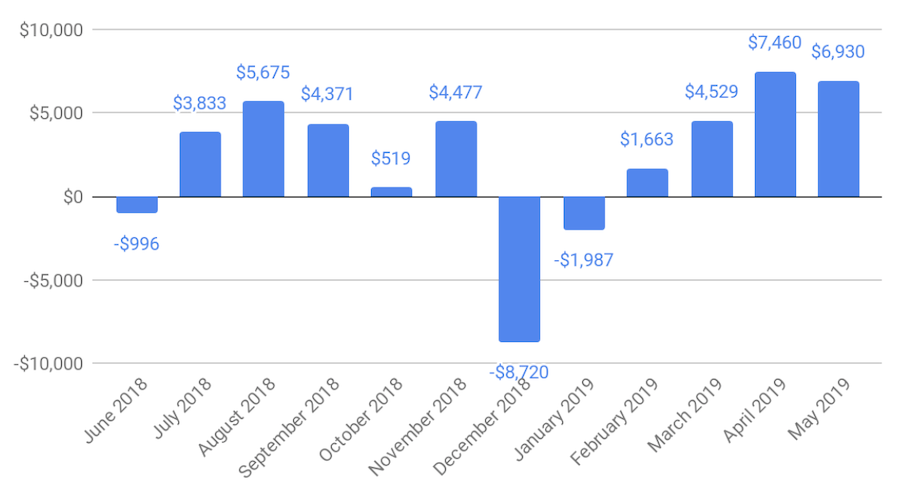
This is what is left in my greedy hands if I cashed out the fund and paid off the mortgage.
For example at the end of June the fund was worth $198,300.01 and my mortgage was $199,296.47. So if I wanted to cash in the fund and pay off the mortgage, I’d need to come up with an extra $996. Wait, what’s that now? I need to pay $996? Oh crap! Terrible decision!
However, by the end of August, I’d have an extra $5,675 in my pocket so therefore I’m a genius. Fantastic decision.
In December the market goes bananas and I’m out eight grand. Again, terrible decision! Wow and this fund is 60% bonds? Can my risk tolerance withstand this volatility?
Not so fast, what about the income generated by the fund?
Investment Income
Let’s not forget that the fund pays out dividends and capital gains, which go right into my bank account.
So far the fund has paid my lazy butt $14,389, which has turned out to be a pretty decent income stream.
| June 2018 | September 2018 | December 2018 | March 2019 | TOTAL |
|---|---|---|---|---|
| $1,581.93 | $1,566.19 | $9,764.21 | $1,476.78 | $14,389.11 |
December was a bit of a Christmas surprise with higher than expected capital gains.
It looks like the fund is crushing it even with that downswing in the market. We need to make sure the income gain is considered in the comparison.
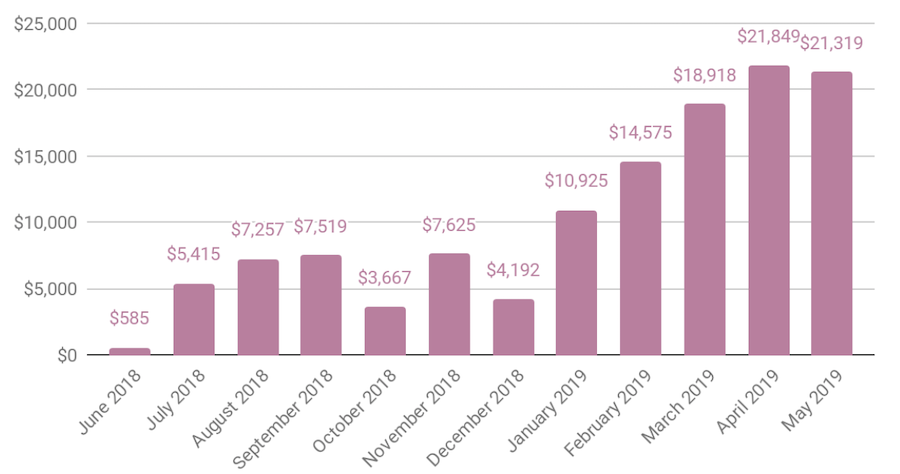
Looks like I’m up over $21 large. Anything else to consider?
Aha! You need to subtract the interest paid on the mortgage.
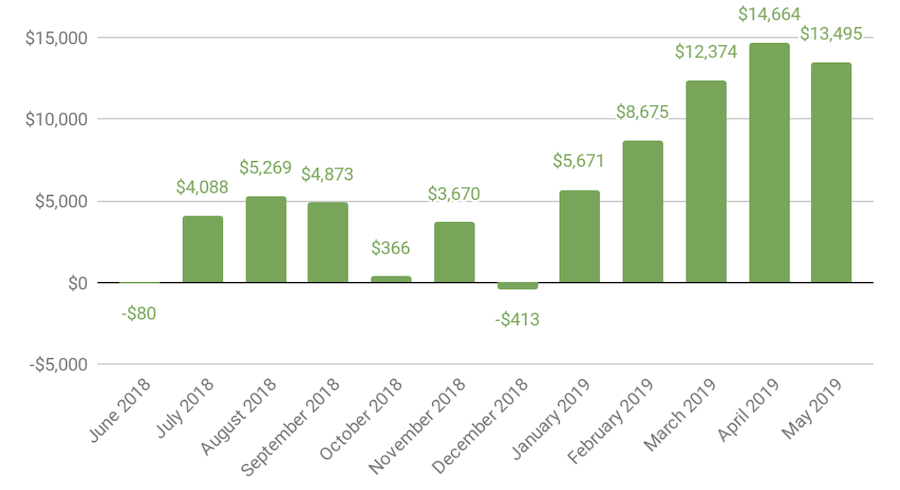
Interest Paid
Every month I’ve got to make a P+I payment to The Man (in this case “The Man” is actually Suntrust Mortgage).
The “P” part of the equation is principal towards equity in the house so I can safely ignore that for this comparison but that pesky “I” stands for interest.
Every month a slightly smaller portion of my mortgage goes towards interest. However, it still adds up.
Over the first year that interest will be $7,823.89 so I need to subtract out those pesky interest payments made for the privilege of using the bank’s money to buy the house.
Taxes
What about taxes?
I’ve purposely left out the tax considerations here.
Historically, tax policy favored keeping the mortgage. However, with recent changes, deducting mortgage interest isn’t the slam dunk it used to be.
There are also taxes that need to be paid on the dividend and capital gain income from the fund. However, that rate greatly depends on other income so for this comparison, I’ll just keep life simple and leave both rates at zero.
Results
After one year the winner is…the fund by $13k!
I think this has shown what we all already know…the math favors investments over a mortgage payoff.
Even this very conservative, income-driven fund is outperforming the mortgage.
However, for many, the psychological benefit of having a paid off home is worth leaving some money on the table.
Trust me, I get it.
For me, having a reliable fund at my disposal that I could use at any moment, for any reason, has some psychological benefits as well.
A paid-off house is great but the only way to get the money out of that house is to either sell or take a loan.
You know what else is great? Having an investment fund at my immediate disposal, especially since it’s also throwing off some income.
Future Plans
What does the future hold?
I’m not sure. Right now I see no reason to change anything and I enjoy tracking the fund performance on a monthly basis so I’ll probably keep this little horse race plugging along for many years to come.
Talk to me after a solid three-year bear market and maybe things will have changed but that is why I chose the type of fund I did.
If my wife and I decided to quit working altogether, we could decide to pay off the mortgage to simplify our finances. However, the fund comes pretty darn close to making the P+I payments for me.
No matter what I choose, I’ll still end up with a paid-off house.
If I stay the course for 16 years and assume a conservative 5% return with 3% income yield, I’ll have a paid off house PLUS a fund that is worth $434k.
Additionally, I will have syphoned off $155k worth of dividends over those years, while paying $74k in interest payments, for a net income of $81k.
All this for NOT paying off my mortgage!
Want to see the raw numbers? My tracking spreadsheet can be viewed here and I update it regularly.
Thanks very much, Clay!
Seeing real-life numbers really helps highlight the differences between the two options.
Although I’d likely go the full investing route myself if I owned a house (especially since interest rates are currently so low), this decision ultimately boils down to a personal choice that you need to make based on your own risk tolerance.
Clay’s hybrid approach seems like a good compromise though, especially since the income from the fund almost covers his entire mortgage payment!
Experiment Updates
Clay plans to update his spreadsheet monthly so keep checking back here to see how the experiment progresses.
Big thanks again to Clay for sharing such an interesting and well-executed experiment and hopefully it helps you decide what to do when you face this same question!




So the reader may be left wondering, why would the bank loan out funds for a homeowner mortgage at a lower rate vs investing in something such as the fund shown here at a higher rate? Risk vs reward.
One reason: secured debt vs. unsecured debt.
Not only secured debt, but also by the way the loan is structured–interest-heavy at the start of the loan.
The interest charged is based on the loan balance.
The way American law works is that a bank must have a 10% reserve on it’s loans. (eg if a bank had 10k in reserves or someone’s savings account, it could loan out 90k) So the bank is not using 200k of it’s money to get a 4% return, its using ~22K (200k is 90%, 22k is the 10% reserve) of your money to get a 36% return (4% leveraged 9x). Technically they are paying you 2% in your savings account, so we will call it a 34% return as long as long as people make timely payments.
Its a fractional reserve banking system.
the bank doesn’t need the amount lended out to the customer, just 1 /9th of it actual (approx). In the US people think the reserve bank prints the money, in reality with the fractional reserve banking system the banks make most of it.
The Hidden secrets of money series video 4 explained it well in video (massive metals lean so ignore that ) (i’m not affiliated with them in any way)
Any longer experiments out there? Been doing mine for 3 years. 70 % in the market low cost ETFs like VTI. Just paying 300 extra a month on mortgage. Market has outperformed mortgage well.
I see money’s job as essentially covering the bills plus having fun. If I can pay out a capital sum to stop having to ever pay a particular bill again – I will as it reduces the mental overhead I have to dedicate to it. Buying a house falls into this category (as does buying solar panels for it).
Buying a house in cash means no more rent or mortgage to pay ever. I got to take advantage of the bank paying me interest while saving and could time the market when buying. Lastly, buying in cash gave me some additional bargaining power with the vendor.
Once bought, I then I started putting the cash saved from renting and no longer saving for a house into my pension and other savings to maximise tax-free returns. That pretty much tracked the stock boom of the last seven years or so making me FI a year or so back.
But I admit that I’m not really a numbers/spreadsheet kind of person and will always work towards lowest hassle rather than sweating my wealth for maximum return.
Look up what Ric Edelman has to say about this. In a nutshell, would you stash hundreds of thousands of dollars in the walls of your house? Of course not, but that’s essentially what you’ve done by paying off your mortgage. That money is no longer working for you and you have no access to it (except with a HELOC, which is another matter). As long as you can invest it wisely and use the proceeds only for mortgage payments, you’re better off keeping the cash and not paying off the mortgage. In fact, as soon as I have my mortgage paid off in about 7 years I plan to do a cash out refinance so I can reinvest all that money I’ve pumped into my house.
“As long as you can invest it wisely” – that’s one of the key questions, isn’t it? Maybe I’m not that interested in spending my time in learning how. Maybe I don’t want the additional mental overhead of managing investments like this or worrying if things go wrong. Maybe I’m too stupid to make good choices in this area, or perhaps I just get unlucky.
For me, it all comes down to what money does for you. I just need enough to cover my basic needs and to have a little fun without ever having to worry. Ultimately, we all have a finite of time to play with and a little extra money isn’t worth it to me.
You are saying you don’t have time to learn investing, but you are here commenting on a blog about financial optimization.
This article lays out the case in real numbers as to how psychology gets in the way of financial optimization. The best thing you can do as an investor is get your head out of the game. Did you know that dead people are one of the best classes of investors?
Read J. L. Collins “Simple Path to Wealth” it a quick read that dispels the complexity of investing. The Mad Fientist also has podcasts with him.
Stop making excuses, take action and learn.
Thanks for your comment, Adam. I rather enjoy learning about physics too, but I’m never going to indulge in real world experimentation in that field. As someone who is FI, I retain a theoretical interest in how others do it.
I already have significant exposure to S&S etc via my pension and enough in cash & other investments to get me from here to retirement age. One of the other commenters mentions Maslow’s hierarchy of needs. I’m a follower of that too – and a fully paid off house as part of being FI means the bottom rung or so is taken care of. Making more money (especially if it involves taking on more risk) will not contribute to my own self-actualisation as far as I can tell. Others mileage may vary.
Nice comment. My sentiment is the same happiness along the journey is a big thing as well.
Do I have the knowledge to invest and make ALOT more money to make the mental overhead worth while? Do I have a grand business idea or somewhere to put the money that will give me a huge return…? Not really, so the mortgage is a good place to go.
However I’m a simple investor, if I can put a portion of money aside for the long term in ETFs for instance, over time I hope it grows for my families future.
Meanwhile I continue to pay an extra portion off my mortgage and if we look to the future over 15 years if I continue both I could be debt free and a reasonable sized investment portfolio.
All the while I have a reasonable amount of income coming into live a decent lifestyle and support my family.
Or that money could be put in riskier investments, continue with a mortgage and take the gamble on where it all ends up…
Your appetite for risk is ultimately going to determine your feelings either way.
I’m taking a similar approach of “meeting in the middle”. I’m sure you can make a mathematical case either way based upon assumptions, but my thought is I need to have enough cash flow to cover my expenses. If I pay a little extra on the principal and invest some – in a way I am diversifying and eventually the mortgage will be paid off and I will need less cash flow to meet my expenses.
I am taking a HELOC and frond loading the mortgage principle. And all my income goes to HELOC. All my parked money goes to HELOC in effect you pay very minimum in HELOC interest as it is simple interest. The simple interest is calculated based on daily average balance. Basically i am using HELOC as my checking account. This way i can pay off my 200000 mortgage in 7 years and and direct my income to investment at that time. Money is not stuck in the house, I can access it any time like a checking account. if the market stay flat then this could be a win. if the market tank like 20% then i will switch to investments. It is nice to have a paid off house.
It might make sense to invest if you have 200, 000 in hand now.
I remember reading a Ric Edelman book long before I know about FI and his whole take on Mortgages had a strong impact on me. Good stuff.
Me too, The Truth about Money.
The interest rate on our HELOC is significantly higher than the rate on a conventional mortgage. And the HELOC has a variable rate provision. We’re using the HELOC to finance an addition to permit us to retire in place because we would have to take out 401K money beyond the required minimum withdrawals, so we are effectively borrowing to avoid selling market investments. But I would not take a HELOC to use for investment in a taxable account.
Agreed! Paid off the house and paid for my solar panels. No house payment no electric bill. My most expensive cost when I retire is my water bill with the internet bill fastly approaching that. The extra I’m saving in these two payments goes to tax deferred vehicles my employer set up. When I do retire because, its no longer fun, my cost to operate are much lower because I’m no longer investing either. The slight amount more made by investing over paying off a mortgage early are at risk for as much as 30 years and with cycles of the market at 7 to 10 years you have about 3 to 4 chances where you might lose your job and the market goes south and you might get forced oout of your home.
Awesome to see this experiment. I’ll add in that fu d he chose was way more volatile than it has been historically over the last eighteen months. I rolled my retired father in law’s 401k into it and have fielded enough phone calls about it!
Pretty interesting article and thanks for sharing. I wonder how the numbers would look if he had included the value of the house vs. the remaining principle. I think any appreciation/depreciation of the house should also be considered against the market fluctuations.
Why? Any appreciation of the house is still captured if the house it mortgaged.
It would be interesting to see appreciation/depreciation, but it wouldn’t have any impact on the value of paying off the mortgage vs. investing.
In this case, including the value of the house won’t change the outcome. In both scenarios, the value of the house would be the same, adding to or subtracting from the net total by the same amount. The value of the house also does not affect the principle value of the loan.
Well you are including the gains in the market for his fund in this exercise right? If the house gained 1 or 2% than he has made money on his “investment”.
If the house gained 1 or 2%, it did that regardless of it being paid off or mortgaged, so it does not affect the scenario. The gains in the market are relevant because they only affect one side of the scenario.
I like the analysis and discussion overall but I’m left wondering about risk in the mortgage debt vs a paid off home. There’s no real way to quantify risk other than mitigating it 100% so for the average joes out there, isn’t there more of a psychological benefit to a paid off home than putting a sizable chunk in an investment vehicle no matter if it’s “balanced” or not? It’s still risk and it should be accounted for. Curious to hear your thoughts.
Hi sullivan,
Modern “conforming” U. S. mortgages are not “callable”. That means: the owner of the mortgage can never force you to pay more than the next month’s mortgage, as long as you pay on time. (HELOCs may be callable, your mileage may vary.)
So paying your mortgage reduces your liquidity – you cannot easily access the equity again, unlike with stocks or bonds – and less liquidity translates into more risk.
The risks you face with any investment don’t change depending on the source of the funds for that investment – you need to examine each risk separately.
My nine reasons for NOT paying off my mortgage early:
1. Mortgages are probably the cheapest loans you can obtain (thanks to government subsidy, government-sponsored mortgage securitization, etc.);
2. Mortgage interest is tax-deductible (YMMV);
3. Mortgage payments become easier over time (inflation favors the borrower, who repays in depreciated money);
4. Mortgages allow you to extract equity without selling;
5. Mortgages allow you to invest more than you otherwise could (mortgages provide some leveraged investment money);
6. Historically, index investing provides higher returns than the cost of the mortgage, especially after-tax;
7. Mortgages provide greater liquidity – you only need to make next month’s payment;
8. The greater liquidity mortgages provide reduces your risk;
9. Mortgages allow you to minimize opportunity costs (cash used to pay your mortgage costs you because you could have invested it more profitably elsewhere).
Buying all cash does not mitigate the risk. It definitely gives you more leverage in a negotiation, possibly a better price, and cuts down the paperwork down the line. That’s valuable, but for most people who put their life savings into their house, it’s also pretty risky on several levels.
I think you should consider paying in full only if:
A) It’s the home of the rest of your life (ie, you truly don’t care about its resale value)
B) Cashflow is not an issue and you could deal with a catastrophic loss. Even with a good insurance, it means you should have enough money available to deal with the contingency until the situation normalizes.
If either statement is not true, you really should treat your home like any other investment, and consider this:
– When you pay in full, you invest 100% of that money into a single, non-liquid asset; which is a significant risk, but one you may balance with other assets in your portfolio (edge vs market depreciation) and insurance (edge vs actual damage). Once you’ve accounted for the risk, it’s perfectly reasonable to value simplicity over financial optimization.
– If you take a loan and invest the money instead, of course you can use the leverage and try to maximize profit; but you could also just edge your brick and mortar investment to maximize safety. It comes down to your appetite for risk, and plenty of wiggle room. This flexibility is particularly valuable if your circumstances change.
Ultimately, it’s a trade-off, and there is no 100% safe option, so you need to do due diligence. Buying all cash is definitely the simpler option, but not the safer or more profitable one; it is the right trade-off for you if you don’t have the time and / or inclination to deal with the minutia.
My concern with “equity” is it just seems like a source of additional debt. Living beyond your means. Then it makes me question buying vs. renting if equity isn’t your end goal. Any thoughts?
Why do you subtract interest?
I subtracted the interest because it is a monthly cost I would not have if I paid off the house.
I kind of think of interest as rent I pay for the privilege of borrowing that giant pile of money the bank gave me.
This is great. Well-thought. We’ve all gone through that brain damage. You did a great job of thinking and acting, and winning!
Thanks!!
Hi. I would like to add paying off a mortgage is a guaranteed 4% rate of return on your own money. The past 10 year return in the market has been great, but you cannot get 4% guaranteed from anywhere. Plus I would no longer have a mortgage payment putting me closer to FI. We save, investment, own rental property, and pay our mortgage down (on an 8 year schedule with 6 years to go). After 20 years in the business of financial planning, a balanced approach satisfies many goals. Just my 2 cents. Thanks.
I love your point on basically earning 4% on a “deposit” towards the mortgage. It is especially apples to apples because paying 4% and deducting the interest at a 24% margin gives an effective rate of 3.08%, earning 4% and paying 24% on the interest gives an effective rate of 3.08% also. That’s exactly how I explain it to others sometimes.
As for guaranteed income though, in 2007, my FDIC Insured online savings account was paying 4.5% and my current 30yr mortgage rate is 3.5%. Even though my savings account now makes 2%, it’s not unlikely that we could see 3.5% or higher guaranteed (of course, investing gets better return)
In 2013, I made the decision to get a mortgage (3.25% at 15 years) and I invested the $136,000 that I could have bought the home with. Fast forward to today when $136,000 invested in the S&P 500 with dividend reinvestment is now worth $277,839 (more than doubled!). At the same time, I’ll pay less than $40,000 in interest over the course of my loan. Of course, I unknowingly picked a great time to do this (Hello roaring stock market!), but I also think that earning more than 4% in the markets over the long term is a pretty safe bet.
Now, if I would have paid cash, I’d be investing all of that extra money each month that wasn’t going to a mortgage payment. I’d still be far ahead by frontloading it all though.
This is a unique time in history for mortgage rates. Heck, I remember when 6% was great! Take advantage!
Interestingly, if Clay chose to pay off the mortgage entirely, then invest the equivalent of the mortgage payment ($1,368.53 per month) in the same fund, and assuming the same 5% return and 3% income yield, his fund balance after 16 years 8 months would be $426k, and he would have earned $92k in income, for a total of $518k, which is very similar to the $515k in his projections. The only risk in this scenario is the ability and determination to make those monthly payments, as the income from the fund is not large enough to make the payments (but getting close by the end). Also, he has access to the full equity in his house (via a HELOC at almost any time) instead of just the portion over the principal balance of the mortgage. Finally, the point about the math being simple isn’t quite that simple: 7% return -4% interest is a net of 3%, but in the paid off situation, it is 7% – 0%, for a net of 7% return, albeit on a smaller balance.
The fund does not win by $13,000 becuase you cannot ignore the tax considerations.
Mortgage: For most homeowners, interest on a $200,000 loan at 4% (together with other itemized deductions) will not be enough to exceed the standard deduction, so there will be no tax consideration on the mortgage side of the comparison. That is only $8,000 in interest versus a $12,000 or $24,000 standard deduction.
Mutual Fund: Dividend and long term capital gain rates for most taxpayers is 0% or 15%. Clay’s fund is heavy in bonds, so the interest portion of the distribution will be taxed between 12% and 24%. Yes, I understand it could be 0% and it could be 37% and there are state income tax considerations as well. For this comparison, I would estimate 20% tax bite on the mutual fund side of the comparison.
That means the mutual fund only wins by about $10k rather than $14k over the course of a year.
>> The “Smarter Than Thou” finance ninja will tell you…
>> “Mortgages are GOOD DEBT! Investments are the way to go. Borrow at 4% and earn 7% in the market! It is simple math you moron. Plus tax law is in your favor. Don’t put your money in the house…put it in investments.”
Wouldn’t it be borrow at 4% and earn at 10% (nominal terms)? Or borrow at (4% nominal) ~1% real and earn at 7%? Saying borrow at 4% and earn at 7% is treating inflation differently across investments, and makes the mortgage look much better than it actually is.
I’m new to FI planning and not a super math whiz (yet!), so forgive me if this is dumb question: How does the massive amount of interest that most people pay on their mortgages affect the decision to pay off a mortgage early vs. investing instead? In other words, if a 30-year mortgage on a $300k home actually costs (let’s say…) $475k, paying off your mortgage (or buying the house in cash) is like “saving” $175,000. Is that the wrong perspective?
Jess,
Great question. You’ve got the right idea. There is a massive hunk of interest to pay on a mortgage.
So in your example paying $300k in cash for that home saves $175k in interest payments.
However you also lose the opportunity cost of the potential earnings of that $300k had you invested it.
I look at it like this. It is kind of like two sides of the same coin. Either pay someone else for using THEIR $300k or someone else pays you for the use of YOUR $300k.
The basic premise presented above is that yes, over the course of the loan you’ll end up paying $175,000 of interest in your example. However, since that $175,000 of interest is based on a 4% interest rate (for example) if instead you invested the money and earned 8% (for example), you would earn much more than $175,000 in investment income over the life of your mortgage.
You’re basically using the bank’s money to earn investment income (because you can earn investment income at a higher rate of return than the interest on your mortgage).
Awesome Job guys!!! Paying our mortgage off is a piece of mind for us that is worth it!
Clay – Since you plunked down a huge nut after minting the mortgage, have you looked into recasting your current mortgage?
Here’s post explaining the difference between a refinance and a recast.
http://threeactionthursday.com/2019/03/28/recasting-vs-refinance/
Paul –
I’ve never heard of this “recasting” witchcraft of which you speak!
Sounds pretty interesting.
When I made the extra principal payment the P+I automatically adjusted to reflect the shorter length of the loan but the total payment stayed the same.
For example my P+I … (may 1 2018) $428.24 $940.29 and after …. (june 1 2018) $703.53 + $665
Didn’t I effectively achieve the same thing?
No, this is not the same. If you recast the loan, the P portion of P&I is reduced in your required monthly payment so the length of the mortgage does not change from the original time. Your $940/mo payment would be reduced versus your last payment being sooner in this scenario. However, you could still choose to pay the same $940/mo and end up paying the loan off at the same earlier time as your example but you would have the option of paying less per month if you wanted to. It gives you more flexibility in your monthly cashflow to recast versus just paying down principle. Some banks charge a fee to recast though, so that is something to consider as well.
I’ve done this — in most cases, you have to request to recast before you make the payment. However, my mortgage company was willing to refund my large sum payment so that I could submit the recast paperwork. It’s the benefits of refinancing, without the financing fees. With a recast, you keep your original loan terms and they adjust the principal balance to reflect those loan terms.
Interesting experiment. If you’re a number person, investing is the way to go.
It’s different for everyone, though. Either way is good.
We’re in the same situation now. We’re selling our condo and could pay off our home. But I’m going to keep the mortgage. Over the long haul, the stock market should win.
This is a great example, but there is one thing to consider – Clay was working with a big lump sum in the beginning and simply deciding where to put it. But most people are dealing with a longer term effort when they’re considering paying off their mortgage.
For many, the goal of getting rid of their mortgage gives a tangible goal that helps them bump up their savings rate in a way that adding to an investment fund doesn’t. At least, that’s what we found in our case. We knew paying off our mortgage might not make sense by the numbers, but the psychological push it gave us to pursue the the principal balance of zero motivated us to save at really high levels. Now that the loan is paid off, we just don’t feel the same drive to throw all the money we can into investments.
All to say, what motivates you can really affect the numbers as well.
My thoughts exactly!
You are correct, but the math still holds for either. In the situation where someone has an extra $500 or $1000 a month to do either with, you’ll still gain more if you have faith in the 4% rule and the underlying assumption that it’ll return 7% after everything in the market. You are right in that there is 199K+ less accumulating for the non-lump sum person in your scenario.
If you put 500 in the market, at 7% over 15 years, you end up at 158K. $1K, you end up at $316K. You could compare either of these numbers over what you get by paying off a specific mortgage early.
One problem I see when discussing mortgages is that people look at the total interest paid and freak out, since it is paid over such a long time, instead of focusing on the _rate_ of interest.
Totally agree.
I wouldn’t say this is much of an experiment, since its basically one year. Anyone will tell you that if the market goes up you will outperform a fixed mortgage and if the market goes down you will underperform. You could basically say the same thing about trading stocks on margin. Is it better than paying all cash? Yes if the market goes up! Hell no if the market goes down.
Chances are the majority of people when “paying off the house” are in reality paying down their mortgage with an extra $100 maybe $200 a month. Not many will get a windfall and be able to pay off in 1 lump sum. As far as being able to pay off from sales proceeds and investing in the market, timing is everything and volatility may be too much for some to handle with the present global/political situation. Too many are still gun shy over the loss to their portfolios and homes in the recession. What makes sense from a rational mindset does not, in many circumstances, translate to one’s emotional mindset.
This was a nice academic (real-life for you) exercise though and I appreciate your taking the time to quantify this example.
Haha, this is an entertaining experiment, however obviously being up $5,675 by August “genius” and then down $8K in December “terrible decision” is intended to be humor rather than evidence to support one side or the other right? I mean picking one fund at the puttering tail end of the longest bull market in history and then a short time horizon is just kind of all noise and no signal. Interesting question and perspective though. Also, ignoring taxes seems like a strange choice because the applicability of the mortgage interest deduction is super important right? None the less, it is interesting hearing from someone who is actually doing it and having a link to follow the spreadsheet over time. Experiment on amigos
The simplification of ignoring taxes would seem to skew these results for most people…
It is very hard to do the math on these types of decisions but ignoring something that takes 20-30% of the dividends and as stated the new limited deductions under the tax law changes the dynamics in my opinion.
I recently paid off my house because of these tax changes – as (for me) it did not make sense to maintain the debt. While it may not have made 100% mathematical sense to do so… the “return” vs the “sleep well” factor balance tipped with the recent changes. I should note I am in the higher end of the tax brackets on income as well which reduces my “return” but looking at a real 1-2% “return” it did not seem worth it to me. I now am investing that mortgage payment and worry a whole lot less about having to make one.
Three years ago I had the option of either paying off my mortgage or refinancing. I choose to refinance the $300K for a 15 year 2.8% interest loan. I put the other $300K into VSMAX (I have a long time horizon, so I don’t mind the risk). VSMAX has averaged 13% over the last three years, plus it has paid about $3,600 a year in income. Every time I hear Dave Ramsey say debt is evil and there is never a reason to keep debt when you can pay it off, I cringe. I would have lost out on the chance to make $100K if I had taken his advice three years ago. Twelve years from now, even if we hit a major recession during that time, there is no way I won’t be ahead when the house is paid off.
You’ve had a very unusual market with a record first half. Catch the wrong part of the business cycle and this could really hurt. You are not accounting for risk. With the yield curve where it is and valuations where they are (Marketcap to GNP, q, CAPE, etc) it is certainly late cycle. This experiment may yet end in pain.
After having lived below my means for 45 years during my professional life, having saved an average of 30% of my income every year, having had several mortgages over the years (starting with a great 16% mortgage on my first house – and yes, there were once days of raging inflation that could still return in the future!), and now finding myself a deca-millionaire, there is one thing I’ve learned about mortgages. Pay them off early!
To convince yourself, calculate the future value of the income stream you’re paying to the bank over the course of a traditional 30 year mortgage and you’ll know why the industry pushes the old maxim “it’s always good to have debt”. It’s good for the banks – not you!!
Now another thing about mortgages: whatever rate you are paying, it’s guaranteed not to change and you are paying with after tax dollars. So if you have a 4% mortgage and are in a 25% tax bracket, that 4% is equivalent to 5.33% before tax GUARANTEED. Every dollar you pay on your mortgage saves paying 4% on future dollars, and so thereby you are guaranteeing yourself a before tax return of 5.33%. What other guaranteed bond or interest bearing fund today offers that? It is always a mistake to ignore the tax effects of your decisions; go back and change those 0% assumptions in your analysis.
Finally, try to make 13 payments in a year instead of 12 (to do so, just increase your mortgage payment 10% and tell the bank to put that extra money towards principal). Then your payment schedule on a 30 year mortgage will shrink to a little over 16 years. Then for the balance of those 14 years (once you are free of debt and truly financially independent beholden to no banks), start putting your mortgage payment into the markets and begin paying yourself and not the banks. Run the numbers and then see what the future value of your equity balance would look like at the end and see what you’ll have: a paid off house AND a huge equity asset in your portfolio.
Just saying….
Completely agree. We are in a similar situation: high tax bracket and already equities-heavy (80/20). I’ve been paying down our mortgage as a way of getting a better guaranteed return on our investment (vis a vis bonds). We already have plenty of liquidity, so I also see it as a no-brainer (for us). Thanks for the alternative view.
This is wonderful information! Thank you for sharing!
Thanks for sharing the experiment. This is always an interesting discussion. Don’t think there is a right/wrong way to think about it either, and doing a little of both isn’t a bad option. Would be a much more interesting discussion if the returns were flat/down over a year or two vs +4% for paying off mortgage. It’s also an apples to oranges comparison IMO. It’s a decision one has to consider, but you are looking at more juicy returns of the stock market or even stock/bond mix, vs a bond (mortgage payoff). FWIW, my wife wanted to payoff the mortgage and I wanted to invest. We made the decision to start paying off the house in 2016 and made our last payment in November 2018. Glad we decided to payoff our mortgage vs invest the money. Returns would have been much better being invested vs paying of the mortgage, but I never think about the “lost money” from not investing because of the peace of mind and flexibility we have now.
I split the difference in our case. This goes to the piece of mind part of the equation. We took a large sum in cash and put it against the mortgage. This will set us up to have the mortgage paid off when we FIRE. We are only talking about 5% of our networth, so we are bot talking about a back breaking sum. It saved about 10 years of mortgage payments. We could pay the rest off, at the cost of most of our non-retirement savings, but that seemed too much. It would take about 15% of our networth to do that. Our retirement accounts value plus equity in our home represents about 79% of our networth. Ideal, not mathematically, but I sleep better this way.
I think you can look at periods of time where each option would be superior. Over the long run (10+ years) going the stock market route is almost certainly going to give you more money. Like the author I chose to do a blend. I have two income properties, one with a 15 yr mortgage at 2.75% one with a 30yr at 3.75%. I treat the 30yr mortgage like a 15-yr mortgages and put the remainder of what I can save into my taxable brokerage account and buy VTSAX.
Great experiment! In our case, we chose to payoff our mortgage after giving it much thought; peace of mind won. We didn’t have a large amount left ~$45k. Four years later, I can say we have no regrets. And our finances our good.
I have a question. The fund seems to be paying out 7.2% however the fund claims a 3.10% SEC yield. How is the author getting $14k in one year from a $200k investment in VWIAX? Is the author including the unrealized capital gains in this calculation? If so that seems like he may be counting those gains twice. Just wondering what I am missing here. Thanks for the post. Enjoyed it.
The huge payout in December was likely also capital gains. Mutual funds are required to distribute capital gains from sales once a year.
I was wondering the same
I see that there was quite a large capital gains payout in December 2018. I didn’t realize that these funds pay out capital gains as I thought they just paid out dividends. That was my ignorance. Please disregard my question. Obviously in down market years this will go away but it is a nice chunk of change.
Everyone needs to make sure they understand mutual fund capital gain distributions. That big December distribution may seem like an income gift, but chances are it is just a taxable event for you without any increase in the fund – meaning you’re actually less ahead than you may have thought. Cheers
Another way to think about it is to consider paying off your mortgage as a guaranteed bond paying 4% or whatever your mortgage rate is. So instead of putting investment money in VMAIX put it all in an S&P500 or Total Stock market fund. So then you can consider it as $200k in a guaranteed 15 year bond paying a very high 3.99% and $200K in equities for a 50/50 split.
The whole idea of if it is better to pay off mortgage or invest is silly as is exactly the same question as is it better to invest in bonds or stocks but the interest rate on the mortgage is higher than bonds.
Excellent comment, seems to me it is better avoid the mortgage (~4%) and shift asset allocation out of bonds (<3%) and into equities. Does it make sense to have bond investments paying a lower rate than your mortgage? Not sure, I don't think so.
This is a nice comparison piece but it leaves out a major factor. When you pay off your mortgage, you begin investing that newly found cash flow, which would generate the same returns in percentages. After 16 years in the writer’s example, you’d still have a nice chunk of money.
I went with the paid off home option and assigned nearly the same amount to investments (529plan, max 401k, HSA and FSA accounts, and a little extra for fun) We still have to enjoy the paid off home!
See I feel like this “compromise” is the worst decision to make. Because you’ve effectively put a large portion of your money into an illiquid asset. If for instance you got laid off you’d rather either have all the money in an account accessible to you or no mortgage payment. Not half the money and a full mortgage payment. Obviously if you don’t need the money at all it’s kind of irrelevant, but I feel for most people the decision to pay or not pay off a mortgage is made during their working career.
This is a fantastically thorough article for those out there like me who need a math-style kick in the pants. I still paid off our house. I can’t say it’s completely without regret, but it does feel excellent to have it off the table. I don’t think about it much anymore, but I’m still intrigued by posts like this.
I am right there with J. I have a similar question. The numbers seem too good to be true…
Hey Savvy,
Glad you liked it! Thanks for the comment.
One of my goals for this was to show a real world example. I like reading articles and understanding concepts but nothing speaks like real world data. Warts and all. I’m pulling the numbers directly from my vanguard account. So the only two fields in my spreadsheet that I update are Market Gain/loss and Income Return per month. Everything else is locked in. (mortgage rate etc)
Keep it bookmarked I plan on keeping this going for as long as I can! Interesting times are coming I’m sure. :-)
A one year experiment is a good start but hardly conclusive. Timing also is critical. We are currently in the longest running bull cycle ever. Run the same experiment in 2007 for a few years and see how that would have worked. You could simply ask all those who went into foreclosure if they would have rather had a paid off house.
As always the correct answer is rarely fully paid off house or fully invested. Diversification would suggest you do a little of both to hedge your bets so you are not 100% wrong one way or another.
Also, most people are not in the enviable position of trying to decide what to do with a house sized stash to invest. The typical situation is that you have just scrapped up enough cash for a down payment and have to borrow the rest in order to buy today.
I currently have a paid off house, using the diversified approach. As it turns out I could have done it faster if I did the fully invested approach so yes the math does work, at least sometimes. If you ask me if I am going to take out a mortgage on my house to invest though the answer will always be no. (same question from a different perspective)
I’m assuming he’s not paying the mortgage bill from his investment fund each month, but rather another income source, so this is not really comparing apples to apples. For the scenario of paying off the mortgage in full, he needs to assume that he would invest the would-be mortgage payment into the mutual fund and then calculate that balance by the end of the year.
Also, one bad year in the market (-20%+) could wipe out 5-10yrs of “savings” with mutual fund. Not to mention the mental and emotional “cost” of knowing you were $8K in the whole for a full month.
If you have the opportunity to have no mortgage…TAKE IT! Mort = Death …gage = contract. It’s a death contract!
Take a look at this home payoff calculator.
https://sites.google.com/site/spreadsheets/spreadsheet-categories/financial-sheets/mortgage-amortization-with-paydown
As I approach retirement (3ish years) I am driven to pay my mortgage off. Some of my reasons to pay off our mortgage rather than invest: (actually in addition to investing)
1) the peace of NO DEBT. I have enough to worry about.
2) the simplicity of no mortgage payments.
3) the certainty of knowing that it’s taken care of. There is no certainty in the market.
4) the security of having the equity of my home “in hand.” The house is tangible. I understand the value.
5) the comfort of substantially improved cash flow.
6) the knowledge that I won’t be leaving my wife with this burden if I get hit by a truck. And I am at high risk.
I understand the logic of investing instead. Psychological needs and safety are at the foundation of Maslow’s hierarchy. I am going to take care of that stuff first.
Great Post! And this is a timely one for me. I do think it is worth looking at over longer time horizons, since as others pointed out, this would look very different if you had paid down your mortgage in 2007 and looked at it in 2009. But over longer time horizons, keeping the mortgage becomes even more compelling
I’ve spent quite a bit of time on this one recently for our mortgage. Hopefully this will be helpful to others. I’ll start by saying that there is a good episode of the Firedrill podcast on this, and also approximately 1,000 threads on the MMM Forum discussing this. I found the posts by ARebelSpy and Nords particularly persuasive in changing my mind from team pay it off to team keep dat mortgage.
First, our specific case. We bought our house with about 5% down. Shortly after, we sold our previous condo that we had rented out (owned free and clear) and paid down our mortgage by about half, leaving ~150K on a 300K mortgage. Previously, I had always thought that close to FI or at whatever point I move to something else non-W2, that we’d cash out some stock and pay it off and not have to worry about it. A decision I’ve always recognized as not the best financially, but the one that reduces our expenses to a minimum and eases any concern about where we would live.
Now, I believe that we’ll refinance and carry a 30 year mortgage to the term’s end and not overpay it at all. What changed my mind? A handful of things. First, a mortgage is just such a special special kind of debt (a bit tongue in cheek here). But really, it is non-callable and fully guaranteed. The lobbying and religion around home ownership in the US is something that I think it worth taking advantage of. Second, the interest rates have gone up, but they are still crazy low historically. I wouldn’t be surprised if they are the lowest they’ll be over the life of the mortgage. Third, and probably the biggest, is that it creates an obligation that gives us maximum flexibility. A bit backwards sounding at first, but what I mean is that it gives us the maximum amount of money in the market to grow, and also reduces the risk that we have a ton of money tied up in a non-diversified asset in a single home that is not producing income. If the goal for us was to invest in real estate, I think we’d be better off with a pure rental property, investing in a syndicate, or a REIT. I don’t view our current house as an investment in that sense. The fourth is FOMOOD. What’s this? Fear Of Missing Out On Debt. After FI, many people have reported problems with getting ANY mortgage since they do not necessarily have regular income, and I’m not necessarily planning on having any post-FI. Preserving the option now means we have it later. The fifth is that this mortgage number is so small at $700 in P+I payments that I don’t have any real concern paying it if everything did go south. I can come up with that number fairly easy (yes, it would be $700 on top of everything else too, but I, still not concerned).
On our particular numbers, I’ve looked at setting aside the principal needed to pay it off, rounded down to 150K and run the numbers. So basically, 25x, 4% for all non-mortgage expenses, and just the 150K for the mortgage, since it is both not subject to inflation and I also don’t care about eating into the principal as much (since we would if we pay the mortgage now anyways). Looking at it simplistically, with it gaining 7% on average over 30 years, that 150K pays the ~700 a month mortgage and ends up more than doubling to around 330K. Of course, this doesn’t include risk at all. If I’m reading cFiresim correctly, there are four scenarios where this wouldn’t have worked – 1909, 1928, 1929, and 1930. So as long as the world isn’t melting, you end up with more money at the end keeping the mortgage.
All this to say that if I ended up well above our number and was willing to overpay today to get rid of the mortgage, I might revisit this, but at this point, I’m strongly in favor of keeping the mortgage.
If you are FI, you could loan yourself the mortgage. Not sure if it’s too circular to pay off your self-loaned-mortgage from dividend-interest-CG income… :)
Might be fun to name your own rate and payoff schedule, and you avoid any appraisal – PMI – etc “hassles”.
When we apply the 4% rule, we are in effect saying that our real rate of return (factoring in sequence of return risk) is 4%. The risk-adjusted return is quite a bit lower than the long-term average return. The 4% nominal mortgage rate starts to look more similar to the possible investment return rate.
There is also the “hard times” scenario. When we hit hard times, often the stock market, the housing market, and the job market turn down at the same time. If the homeowner suddenly loses their job, they must still pay the mortgage each month and failure to do so leads to all kinds of bad things. Selling off investments or the house during such hard times means that we are selling at a loss. Selling investments also can generate tax costs when we should be trying to cut costs.
I think they small opportunity for investment returns (risk-adjusted investment return – mortgage interest) is outweighed by all these risks. Better to pay off the mortgage. Cash flow improves (P & I), and expenses are reduced (I). Less investment is needed to hit the magic 25x expenses and FI comes sooner.
I think I am missing something in these calculations. The Vanguard website shows that the returns after taxes on distribution is 5.34% since fund inception in 2001 (yes this number is higher in the past year only.).
If my mortgage is 5%, which actually closer to 7% when factoring in state and federal taxes since I am using after-tax money to pay it, wouldn’t it make more sense to pay down the mortgage? What am I missing in these calculations?
My rule of thumb, having been at this for 25+ years, is if the interest rate is 6%, pay off the debt ASAP or avoid taking it in the first place. There are two other factors to take into account though. Do you have a 3-6 month emergency fund? The other is, are you in this for the long term, 5+ years at a minimum. The above example is for 12 months in a very good year. If this was a 12 month example in a down year, it would be cutting it close. An average year would still show the advantage. So, if you are looking at a 5, 10, 20 year time horizon and you have a 3-6 emergency (cash) fund, go for it! I have closely tracked this myself in Excel for over 20 years (through many MSFT upgrades with the same spreadsheet) and it just works, period.
I have some great books on my shelf written about (not by) Warren Buffett and how he accumulated so much wealth. Unfortunately, his unorthodox ways rarely make the “get rich quick” circuit. I wish there was a “get fabulously rich slowly” circuit. But here is at least one link to his reasoning behind using a mortgage: https://mortgagebite.com/mortgage-blog/personal-finance/even-the-rich-get-mortgages-warren-buffett-explains-his-mortgage-borrowing-strategy-to-cnbc
It is simple, but totally worth the read for someone that has been at it for over 70 years!
To Karen C.: In my experience (not just in my opinion), it is ALWAYS better to not have a mortgage for so many reasons: peace of mind, freedom from debt, availability of options when crisis hits. Anyone considering entering retirement or becoming financially independent early while still carrying a mortgage is foolish.
The book I read nearly 40 years ago was “Money Dynamics for the 1980s by Venita Van Caspel”. You can still find copies around. Though written for a time when we had just come out of stagflation and walked right into a period of very, very high inflation, some of the narrative may seem a bit outdated and foreign today – but not the basic concepts and principles of getting out of debt and paying yourself first. But recognize now that today in the year 2019 we have a government with over 22 Trillion dollars in debt (with much more than that in unfunded liabilities), a shrinking tax base, yet increasing obligations. There are only two ways out of this situation in the long run: high inflation and/or high taxes. Don’t be lulled into complacency based on your short term experiences (e.g., interest rates will always be low, taxes will always be low, etc.): look at the possible long term scenarios and plan accordingly.
But if you get the right attitude set now, stay on course and patiently apply the principles outlined in that book, you will find it EASY to build a multi-million dollar portfolio to weather the storm and hunker down in your paid-off house. I did it and so can you.
Great article! I can totally see myself in a similar position down the road, especially since my current mortgage is already with SunTrust and my brokerage account is with Vanguard. I’ll definitely be checking back in 2-3 years to see the latest numbers. Thanks!
The Story of Captain Bernie and Captain Jan
My first full month on line as Pilot was April 1994. Back then you flew a whole month with the Captain unless of course he/she was on vacation. That was my case. Captain Bernie flew the first trip of the month with me and during informed me he would be gone on vacation the next two. I would get a vacation relief line Captain during his absence. Sure enough the second week Captain Jan showed for my trip.
After the initial briefing Captain Jan asked me, “How old are you?” I replied, “I just turned 28 last month during my new hire check ride.” Captain Jan then said, “Wow! You are going to make a ton of money. What are you doing with all your money?” New and not wanting to upset him, I replied that I had just purchased my first house – a 2,200 square foot 4 bedroom 2½ bath house for $125,000 in Arizona on a 30 year VA note of 7.5% with no money down. I then told Captain Jan I was paying an additional $288.27 a month to pay it off in 15 years. Captain Jan said that I was going to need a tax write-off and that I should be investing the additional $288.27 a month rather than paying down the mortgage and losing my mortgage interest deduction.
Back then, we didn’t have cell phones or pads with apps, much less even a laptop we could carry with us. All we had were desktop computers and ledgers. I told Captain Jan that my father was an accountant and I would be happy to go home after the trip, and compare the two scenarios – his and mine. We agreed on some interest rates and the premise that after I paid off the house in 15 years I would take the entire payment plus the additional payment and invest them both in a mutual fund.
I came back next week to fly with Captain Jan. Again after the briefing he asked what I found out? I told him that he had won. He had $5,000 more than me after 30 years. He then told me I told you so. I replied, “Yes sir, but at the end of 15 years I can lose my medical (unable to fly) and flip burgers at Burger King and stay in our house.”
By the fourth week of the month Captain Bernie returned from his vacation and asked me about the last two trips. I told him the story. Captain Bernie said to me in his subtle voice, “You keep doing what you are doing, Frank.” So I did.
I didn’t think much of Captain Bernie’s statement until 2003 when I returned to Training for a Proficiency Trainer (PT). Back then Proficiency Checks (PC’s) were given by Check Airmen and PT’s were given by Instructors. As I entered the briefing room there was Captain Jan who, I knew was a Check Airman. I thought, oh no I’m in the wrong room because I was due for a PT. Captain Jan, stopped me and said it was the correct room, but he was now retired, (this was when age 60 was the limit), and was back working as an Instructor.
A year later, my friend, Captain Bernie retired at the age of 57. I then realized that Captain Bernie knew something. So I called Captain Bernie, I called Captain Fred, I called Captain John, and I called a few other Captains, some of whom were previously divorced, yet all had retired early. I asked them what they felt enabled them to retire early or be financially independent? Guess what? The common denominator among these aviators was that their primary residence was paid for. Oh boy!
Clay,
Please explain why you fully discount the principle as if it is not material to the calculation. You also do not provide for the future value of the interest you are paying that would be available for investment if you had no mortgage.
To do a pure future value comparison you need to express the future value of your expenses that would be eliminated in the alternative case. Thus you should compare the future value of the invested money not put on the mortgage and the future value of the amount of non investment income paid to service the loan(IE total payments-dividend from invested 200k) after investment.
Without the future value of the expenses you are comparing a future value to a current value, which never gives definitive results.
Matt,
I excluded the principle because in my mind it would be a wash either way. The value of the house is the same irregardless of mortgage.
With a mortgage I gain more principle over time. Without a mortgage I get it all at once.
Either way its the same asset. And its an asset that doesn’t really matter for this comparison since it doesn’t generate income or benefit me in any way unless I sell the house or take out another loan.
At the end of the run (16 years) the house is paid for no matter what.
RE: future value.
You are right. I didn’t include FV because it is beyond what I could comfortably understand. I fooled around with trying to compute FV of the lost opportunity cost and comparing to the predicted Fund gain. I just got lost so decided to stick with hard numbers. (those columns are still in my hidden in the spreadheet. Take a look and tell me if I did it right.) This is why comparing the two options isn’t as straightforward as some people think.
Clay,
using your hidden columns I would change from using the FV formula to using your own data as you did all the work to create a functioning case study. so I would alter the formula in column T to be starting in T5 to be “=(H5/G5)*S5+((G5/G4)*S5-S5)+S5” this will give the appreciation for the month of the payment and dividend if applicable for the month. I would change column U in U5 to be “=T5+(U4*(G5/G4))+(U4*(H5/G5))”. This will give you a rolling appreciation of the previous opportunity cost at actualized gains of the stock you own. your future information in the column will have the same assumptions in column J of 0 appreciation until it happens but will continue to show the affect of the payments needed to service the loan.
This would make the June 2019 cumulative FV of the opportunity cost $2,016.28. The June 2019 gain on investment is $3,116.63. Total Gain/Loss on this option versus a paid off Mortgage is a Gain of $1,100.35. Dividends were used to service the loan and reduce opportunity cost. Based on the ending balance as of June 2019 appreciation on your investment was 1.15% without dividends, which is low for this fund. So the fund would only have to nominally perform to start making a large difference in total Gain.
Given this the Cumulative FV in column U will be $258,544.16 with $200,000.00 in principle and $74,318.77 in interest paid, totaling $532,862.93. However at a general gain of 6.8% in 16 years $200,000.00 would appreciate to $573,020.31 giving a gain of $40,157.42. This is before all the dividends that will further reduce the cumulative FV value of the opportunity cost, each year the spread will continue to grow.
In my opinion after this you will have a great case study with hard data that investing the money would be worth the added risk.
Forgot to mention that a $1,100.35 gain on $2,016.28 cost would be a gain of 54.57% in one year. That probably should have been the leading note.
Matt,
I made the change! Can’t say I completely understand it yet but it is updated now!
Thanks!
Hi Clay,
Followed up on this to see how the tracking was working. It looks amazing.
Based on the updated numbers through November 2019 your investment (up $9,885.09) is outperforming the opportunity cost (up $7,589.74) by $2,295.35. Meaning going this route has returned a 30.24% higher return then if you paid it off and invested the same amount of cash flow at the same real time intervals as the mortgage payment. I look forward to seeing this progress further. So far it is working exactly like I thought. Thank you for providing all this data.
You may want to Column V be the difference between the gained amount and the opportunity cost so you can easily see the difference. A simple subtraction formula of column J minus column U provides the number.
One problem with this is that Clay (and MadFientist) didn’t convert the return of the investment to a “Real Return” – the interest rate on a mortgage is guaranteed, it’s fixed in this case. But the return of the investment fund is without accounting for inflation. Mortgages aren’t affected by inflation, but portfolio investment growth is. There’s a more specific formula to be exact, but you have to subtract 2.9% from the investment return to get the actual return an investor will “realize” – this is known as the “real return” in this example Clay would come out $13K ahead but his $13K would only be worth ~$10K (I totally just guessed, not going to run the calculation tonight). The point is your future $ amount is always lower. The real return on a balanced fund that’s only 38% in stocks is going to be closer to 3-5% over the long-term – dang near even with the mortgage interest. And for most people who don’t have the $200K to put on the mortgage and invest, the mortgage will be a huge debt accruing interest while your investments will be small making slightly less or slightly more with the real return, so likely most people without a windfall like Clay had will actually be going backward. Any thoughts on this?
Dan,
Everything is affected by inflation. Inflation would have to be applied to the interest as well as the interest is Future money (IE paid later) so it would be discounted compared to today’s money. The principle is also affecting by inflation as the total amount owed is not paid in today’s dollars but in dollars each month until 2035. if you ignore inflation and put all money as of the time the loan will end you are comparing all costs and gains at the same inflation rate, thus it need not be calculated since either option will have the same inflation effect. Additionally, inflation is less than 2% for the recent past. 2.9% is way higher than we have seen for years. it is true that the return inst what is called a real one but this discussion is more about which one will generate a higher return in the future we don’t have to back out inflation since we are never bring the Money back in time to today to say it was an X percentage gain.
Counting for inflation is vital if you are figuring out what you need to provide for your retirement or spending but inst required in a asset comparison model that only provides the better return unless the returns are not stated in the same time frame.
We are actually living out this scenario as well, so it was an interesting read for me. We had our mortgage paid off in full, but went back into $75,000 of debt to build on a garage/workshop. This was a cheaper option than moving. We had the money in the bank (VTSAX actually) to pay cash. Our investment was making more $$ than what the mortgage was costing us when we ran the numbers out. It was a difficult decision to take out the debt for me (not so much for my husband), just because of the risk. Our payment is very low and we still save 70% of our income. Will we regret it in 10 years, who knows? Nothing is guaranteed… This post has motivated me to go back to last year and run the numbers out for the year to see if it’s paying off for us.
Enjoyed the Cake homage.
Who doesn’t love CAKE!! :-)
I paid my house off (~$550k) a few months ago. I can’t overstate the stress relief, particularly with the markets being more volatile than usual since last December, and doubly so once I was just over the threshold of “I can afford to pay it off if the markets don’t go down any more”.
When making the decision, I simply asked myself “Would I borrow $500k+ right now to purchase stocks?”. The answer (at least for now) was no. I borrowed that money in the first place to purchase a house, which is more worthwhile and fulfilling to me.
For what it’s worth, my FI spreadsheet says that paying the house off added only about 1/2 a year to the goal post, assuming modest returns and SWR.
Great article! Love the mathematical rationale, and yes the fund wins on the right (>10 year) timeline. But for me a little more peace of mind comes with a balance or as you said, compromise. Our thinking was, We worked our butt off to kill that dark cloud of debt! And by no means, let debt grow. I was in Tech during the dot.com days and for about a New York second, I had enough money to pay of my mortgage, then it what seemed like a blink the market rolled over, I had no rules on selling, ignored bubble-theory and I lost the value of a house. After some teeth grinding and reflection, and a few well time Bill O’Neil books, I decided that after monthly expenses, which included a maxed out 401k and 10% to the portfolio, 50-60% of what was left went to the paying down the house. 8 years later, the house is paid for and 40-50% of our income is going right into the market / savings. Another 8 years slide by and hello FI.
There are lots of ways to skin the FI beast, but to me, the foundation is eliminate all debt, live below your means, spend like a Cait Flanders and get persistent and lucky with your funds / investments.
And MF, come back to Colorado and drink the good micro-brew beers with us at MMM HQ!
I could have used this post and its comments a few years ago. I used to follow Ric Edelman as others have, and find it hard to argue his logic. In the end, I was psychologically biased in that I just wanted to be debt free. My wife and I decided to pay our mortgage off quickly.
Of the tools I found, I thought the mortgage professor spreadsheets were very helpful. https://mtgprofessor.com/spreadsheets.htm
I wrote about our path to paying it off in my blog, link below:
https://www.forgingfinance.com/2019/02/10/paying-off-the-mortgage-part-1/
https://www.forgingfinance.com/2019/02/10/paying-off-the-mortgage-part-2/
Here is a calculator worth looking at on this:
https://www.vertex42.com/Files/download2/themed.php?file=extra-payment-calculator.xlsx
Great post! It’s content like this that make me question whether we should actually GET a mortgage. A lot more factors in that decision but this is helpful, Clay. Thanks.
I’ve decided to buckle down and pay off my mortgage. We are two high earners, so I should be able to do it in 2 more years. (Total of 4 out of the 15 year mortgage). For me, this is the right decision for two reasons.
1. After it is paid off, I will feel ready to pull the trigger and retire (or go part time, or take a different job). Our expenses will be low enough that I will feel free.
2. While the numbers may make sense over a long time, (or over the last year), you don’t know what the random walk of the stock market will do. So, if I wanted to pay off a 30 year mortgage in 20 years, I don’t think it would make sense, because I’d have a much longer period for gains, but in two year period, the risk of ups/downs is much higher.
I’m still investing 401ks and Vanguard (cutting back about 50% of VTSAX contributions) during this period. Once I’m paid off, my cash flow will be even better, and focused on Vanguard even more while my spouse keeps working.
So here is a thought not readily contemplated above. In California at least, ones first mortgage is a “non-recourse“ loan. So if you pay off your house first, you are assuming all of the risk if something dire occurs. Like an earthquake. A big earthquake. Civil unrest. Other horrific black swan perils. However, if the bank holds a large loan against the value of the house, they are assuming the risk. If the big earthquake strikes, and your home along with thousands of others are destroyed, you can simply walk away from the property. And if you had invested the money in a diversified fashion you could start all over again in a different location.
Other positives include the fact that the house raises in value independent of the equity in the home. A rise in value of the home of 3% on a $400,000 home is $12,000. If the loan value is zero, this is a 3% return on investment. If the loan value is $400,000 the return on investment is infinity.
Here is yet another reason to maximize the mortgage on the house at all times. Say there were two identical homes, each worth $100,000. say the market tanks, and On the first home, the mortgage is $90,000. On the second home, the mortgage is $10,000. If both homeowners lost their jobs, and could not make their mortgage payments, who do you think the banks would forclose on? Answer of course is the person who only had $10,000 left on their mortgage. The bank could dump the house for $10,000 and recoup all of the loan amount. This really happened in Texas in the 2000s . Apologies for poor grammar and syntax, this is dictated by Siri.
It is what we did last year when we pulled the FIRE trigger. At first I was going to buy the property in cash since we had it; and after the math part of my brain got activated, I placed all the money at Vanguard and took the loan. Best decision so far. Liquidity is high, interest on loan is low enough and I feel better about it since I am not risk adverse or think that all debt is bad debt. I can always pay off the loan with the money we have invested; but, why? VTSAX all the way!
Ricky
“math part of my brain got activated”
That is hilarious. Its definitely a left/right brain problem.
Like you i’m not risk adverse and am ok with debt if the math brain thinks it makes sense.
I kind of like having a pile of money at my disposal that is sending me a check every month.
But…… You just have to be ready to pay that loan off (or make some other change) if the economy takes a dump.
Comparing a single year of investment returns isn’t helpful, given the variability of returns year-to-year. A much more reasonable analysis of this issue was done by Big ERN here (spoiler: he comes to the conclusion that paying off the mortgage is better for mitigating tail risks, e.g. a big bear market right after retiring):
https://earlyretirementnow.com/2017/10/11/the-ultimate-guide-to-safe-withdrawal-rates-part-21-mortgage-in-retirement/
I’ve take a different approach to this. I have 10 years left on a 15 yr mortgage I’m saving enough cash so that the interest on 5 yrs CD’s will just about cover the interest paid for the rest of the mortgage if I am able to continue getting over 2.5% rates on the CD’s for the next 10 years. With this approach I get to keep cash on hand as an emergency fund, have the interest from CD’s cover the interest of the mortgage and not have to be concerned about any potential losses in the stock market over the next 10 years.
We paid off our mortgage last August and I haven’t regretted it for one second. If stocks weren’t at an all time high maybe we’d invest instead of paying down the mortgage, but I really believe that a big dip is coming at some point and it will be interesting to see how people react. Either way, this is a great case study and I appreciate the real life perspective.
I paid off my home versus investing because: 1. Already ave alot saved in ROTH,SEP and 401K after maxing out what I could over the years while paying a mortgage. 2. Wondered if work or my health would change causing me to stop working for a period of time. I did not want something like that to take place with any debt on my plate. What came to fruition was my mom suffering an unexpected, massive stroke one day and passing within 12 days. Dad suffered several heart attacks and pneumonia 1 month later and is now on hospice. Not nearly enough money to hire full time care, I took advantage of being 100% debt free by quitting my corp. job and moving in with my parents during their end of lives. We had fun, connected as adults and I helped them keep their dignity and quality of life that no other medical personnel could bring. There are no investments that would be worth staying in debt and missing out on spending so many great moments with my parents. Everyone speaks of money advantages to not paying off their mortgage, but I never read about the FREEDOM debt free brings to react to the medical crisis, divorce or layoff horrors that pop up unexpectedly to folks at one point or another. It is about hanging on to control to one’s life that only being debt free brings, something I have found to be far more valuable then dividends or capital gains can offer. Just something to think about…I have no regrets. I knew I would have many, many more years to earn more while continuing to grow my existing balances. I also knew if I did not choose being debt free, the freedom to choose no work and living with my parents would never have happened. I would be saddled with so much guilt and regret that would last the rest of my life. I am guilt free, debt free and getting closer to being work free for my remaining years. Hope this different perspective helps!
That’s great that you were able to do that for your parents. However, you would have the very same freedoms if you had sizeable invested funds rather than a paid off house. Most likely more.
Being this is MF’s site I’m surprised more people aren’t talking about taxes. What if the mortgage interest isn’t enough to claim? But instead of putting extra principle in with your house payment you invest it in a traditional IRA or 401k to reduce your taxes to a lower tax bracket? If you are in a lower tax bracket are you fully funding a Roth IRA? In theory at a future date you could take the principle out of the Roth to pay off the mortgage. Or if you are worried about liquidity don’t send the extra money in with your house payment but invest it in an after tax account. Again pay it off when you have enough OR just let it keep growing – Give yourself options. How secure is your job or company? What helps you sleep at night? If you lose the house do you have some place to stay?
So many options to consider that everybody needs to evaluate their own circumstance and make the best decision for themselves and their families. Pure logic and history shows the market is typically better. But with the market on the high side and the 10 year average on the high side is that still the case?
I’m frankly surprised by how many of the commenters have chosen to pay off their mortgages rather than invest. It really is a no brainer math-wise to invest instead but I guess a lot of people can’t stand the thought of any debt no matter how favorable it might be.
Another factor not mentioned is how long you plan to stay in your house. I do not plan on remaining in my current house after I retire within the next 9 years. I live in California where the prices are very high and thus I have a rather large mortgage. I keep trying but I can’t find any motivation to put extra into my mortgage. I’d rather those extra funds continue to grow in VTSAX rather than putting them into my illiquid 3.25% sizable mortgage.
When I do retire, will I pay cash for my retirement home? I don’t know. I will have to re-evaluate at that time based on current interest rates. Or maybe do the same experiment as this article subject and split the difference.
Steve.
Do the experiment man! We can compare and contrast!
A single outcome does not tell us much about the overall risk of each scenario. You really need 100 guinea pigs that pay off the loan and 100 that do not. Then see how many of each did better. Part of deciding whether to pay off the loan is what the risk is for trying to do better than the sure thing of paying the loan You are certain to not pay the future interest, but you may do better or worse than the interest rate if you invest. The decision comes down to the odds of doing better.
When the loan rate is higher, the chance of making more money by investing is low. It is probably better to choose the sure thing at that point.
Sometimes I think the FI community focuses too much on the math of what happens “on average”. Assuming you’ve hit your FI number and quit your job the fact that, on average, you’ll be better off investing than paying off your house is somewhat irrelevant. What I (and I assume many others) am most concerned with is having to return to full time work. Having a paid off house is a nice way to hedge against having to return to work full time. When a market downturn eventually happens, and you factor in sequence of returns risk, I think a lot or early retirees are going to want to minimize the liquidation of their retirement funds and supplement their income with income from a part time job. It is a lot easier to fund (or supplement) a mortgage free lifestyle with part time work and/or side hustles.
Another important thing to consider is your ability to manage taxable income. A mortgage based lifestyle requires more annual cash flow and that cash flow often translates to taxable income. Having a mortgage may make it more difficult to realize the amazing tax benefits of things such as ACA subsidies, the EITC, and the refundable child tax credit.
The “math” may lead to some foolish conclusions if you are hyper focused on the average and ignore the variance. Nassim Taleb is great reading if you want to learn more about this concept.
I would definately choose mortgage freedom. I’ve paid off my townhouse now for a few years and it feels good.
Still have to pay taxes and I choose to insure it. Gives me peace of mind.
On another note…I’m hosting Playing with FIRE showing in Hollywood, FL (smack in the middle between Fort Lauderdale and Miami). It’s on TUGG.com for Aug 27th @ 7:30 pm at the Regal Oakwood 18 Cinema. Tickets are $11 bucks. Need 70 out of the 85 b/c 15 tickets have been reserved! Please promote if possible. There’s a post in Facebook ChooseFI South Florida and also on Instagram.
Thank you,
Nevada Smith
Thanks for posting. I did see you in the film. Funny how the wife pushed back on the $5,000 humble car. Then, she totally embraced it. I got a laugh about it and saw how great that she became so flexible.
One point that I haven’t seen mentioned is liability for anyone with rentals. I have 5 rentals (2 duplexes where I own both units under 1 mortgage, and half a duplex that I own outright) and in FL there is a homestead law that protects one’s primary residence from lawsuits. I have about $236k left on my primary mortgage but intend to refinance the one paid off rental and take that money along with savings to pay off my primary mortgage in 2 years. This gives me liability protection from tenant lawsuits as the rental is protected through debt and the primary house is protected by law. If I had a taxable account with the same amount of money it would be fair game in a lawsuit. My wife and I have chosen this route even though it may not give the highest return it does increase our liability protection and reduces our cashflow needs.
Another point to consider is if your primary house has considerable appreciation it can be sold to reap tax free gains. You can’t get tax free gains with any other investment. Then take the money rent for a few years till the market cools off and continue to rent or buy again.
I’m about to get a second mortgage at 4% to pull this off. Unfortunately I won’t have the tax benefit, but I intend on putting the money in an after tax 401k so then I will have tax advantages.
I’m in a similar situation. Recently got married, sold two houses (mine was all paid for) and relocated 10 hours away with a new house. After crunching lots of numbers, I put some of the money aside in an emergency fund, put a large chunk down on a refinance at 2.99% VA loan to reduce our payments by $1,300/mo and invested the rest in Vanguard, mostly VTSAX which has lost $1,200 (as of yesterday) since I put it in at the height of the market last month. :-( My hubby also bought a new F150 with all the bells and whistles to pull our small 5th wheeler camper but got it a 0% interest. His truck payment is bigger than our mortgage payment now! I’m thinking of putting another big chunk down on the principal of the new mortgage to reverse the the P & I payments so that more is going toward principal than interest. He’s 60 y.o. and so we’d like to pay it off before he retires. If we put another $400 toward principal each month, we should have the house paid off by Sept/2025. My family wanted me to just pay off the house but I chose to split the difference and with this plan will only pay $5,300 in interest over the course of the loan (instead of $54,200). I just hate paying interest to banks! So…. I’m half emotion, half wisdom. We’re betting on us staying healthy and doing some RV travel while staying in our home for our retirement years. Health is Wealth and retirement is just around the corner. I just hope the market investments will do better in the long term….
“The “Smarter Than Thou” finance ninja” in me tells me not to get into the same experiment.
By having Mortgage and investing in Bonds (about $120k – 60% asset allocation out of $200) you are borrowing from the bank with 4% (mortgage rate) and investing in bond with an approximate 3%(or less) yield.
Essentially, you are paying 1%( 4%-3%) of $120k = $1.2k / year to your mortgage Co for the “benefit” of liquidity you have in your bond portfolio. And prior to the experiment you did not really have liquidity problems.
That said, I see only 2 options that make sense to me:
1) Invest 100% in stock and do not pre-pay mortgage. Bank on the risky 7% long term gain.
2) Pre-pay mortgage and guarantee 4% income on your $400k (or less to address liquidity risk)
Both, good options in my view.
I don’t think it’s even a discussion – but as you said, we kind of expected that. Even if the results were break even, your money is liquid in the investment and not easily accessible tied up in the house. I’d even venture to say, it’s smart with rates so low right now to refinance, pull the money out of your house, and invest it in stocks (especially now, as stocks are taking a dive).
http://www.somedayextraordinary.com for more thoughts.
I started with investing and paying the debt on schedule (20 years).
But then I was mentally too weak to resist the temptation of paying off the entire thing once i had the amount invested.
In retrospect it would have been better to stick with the schedule and keep the investments.
A few other thoughts: might paying cash for a new house encourage you to buy less house? I think leveraging 30 years might convince you to buy more house than you need. Also, insurance can be reduced based on what you think vs what the banks thinks. In addition, tax and insurance escrows can be invested vs sent to the bank each month. I paid mine off and don’t look back for the peace of mind, it seems to be everyone’s goal around me to “one day pay off the house.” I can never be foreclosed on. I always hated the bank having leverage on me, hated owing people money. But as others said, I place a premium on living a simple life. Thanks for the article!
“I can never be foreclosed on.”
Not exactly. You can’t be foreclosed on by the bank because of the mortgage, but the government can foreclose on you for a tax lien and they usually aren’t impressed by the amount of illiquid equity you have built up. It also isn’t unheard of for there to be liens placed on homes due to other outstanding debt, medical expenses, etc.. Tying your money up in the home can be riskier in these cases than if you hadn’t.
I am just a beginner in all things money. However, this scenario is my current dilemma. I’m 57. 3.875% mortgage loan with balance of 55k. I think time is not on my side. I need the security of a paid off home. Currently paying 1k/month to pay it off before I’m 62. Am I wrong?
Are you paying an extra $1,000 per month or $1,000 per month total? If you are paying $1,000 per month extra, I would stop and save/invest that $1k per month. That is +-$50,000-$60,000 you would have when you turn 62. You could then keep that money in a separate account to use solely toward mortgage payments or emergencies. For me, I would rather have the cash accessible rather than locked in the walls of my house.
Did a quick spread sheet with and w/o the opportunity cost of interest being paid. and pay off the mortgage and invest the payment. They are so close, what am I missing. Looks like there is not a argument. Please tell me what I am doing wrong here.
“Initial investment – 200 k (mortgage left) at 4% 15year fixed
Interest payment – 4.4k average, opportunity cost from 4.4k
The return on 200k is 8% subtracted by th 4.4k interest payment + the oportunity cost from the insterest payment
W/ opportunity cost” w/o opp cost Payment invested
$200,000 $200,000 $20,412
$211,248 $216,000 $42,457
$223,396 $233,280 $66,266
$236,516 $251,942 $91,979
$250,685 $272,098 $119,749
$265,988 $293,866 $149,741
$282,515 $317,375 $182,132
$300,364 $342,765 $217,115
$319,641 $370,186 $254,896
$340,460 $399,801 $295,700
$362,945 $431,785 $339,768
$387,228 $466,328 $387,361
$413,455 $503,634 $438,762
$441,779 $543,925 $494,275
$472,369 $587,439 $554,229
I am late to the game here but I was also in the keep the mortgage camp until 2008, when I lost more money on the market than the remaining balance of my mortgage. I felt so dumb and everyone around me was losing their Jobs to boot. It was one of THE most stressful times in my life and don’t care to relive it.
You can at least still live in a house that is worth less than what you paid for it. The investment money is just gone for an indeterminate amount of time. Not sure how many commenters aren’t old enough to have lived through a real Recession but it can be ugly. I’ve lived and worked though 3 pretty big ones. Often when you need the money the most, the market is at its worst. Yes, it’s more liquid but if that investment was just worth $1 and now you only get 50 cents if you need to cash it, that doesn’t feel good either. It is a lot less stressful when your fixed expenses are low at a time when your job may be at risk.
I had just started contributing to my 401k a few years before 2008 hit, so I can certainly relate to how you felt back then. However, what I don’t understand about the “pay it off early” strategy is what do you do when a recession, layoff, etc. happens during those many years required to pay it off? You don’t get any cash flow benefits from paying off your mortgage until it’s completely paid off, so it seems incredibly risky to me to give so much cash back to the bank versus the alternatives. Someone could hypothetically send the bank a huge extra principle payment that could cover months of expenses, then lose their job, and they now don’t have that money to pay their regular mortgage payment, taxes, etc.. If you have an emergency fund to cover that, then you’d have that for the case of investing in stocks as well and thus wouldn’t have to sell those stocks at a loss, and if you did hit that point where you needed that money, 50 cents on the dollar from those stocks is still much better than zero from the money you gave back to the bank.
Good point Dave. I also had an emergency fund (2 years expenses) that would cover the mortgage balance if I lost my job. The efund came before the house but I guess it’s not always a given to do things in that order. I agree, I wouldn’t want to go into foreclosure with a bunch of extra principle that the bank could take back if I fell behind on payments. My point was at the time I felt like I had too many eggs in the stock market basket.
While everyone was high fiving about how much they were making, for me it was like watching someone blowing into an already overinflated balloon and feeling more and more anxious the bigger it got. This latest correction has me feeling a sense of relief instead of panic. (Partly because my expenses are low and I Live in a paid off house. I could work minimum wage and be fine if I had to).
Interested to see if this analysis gets updated. Would love to see if opinions have changed now that we are in bull territory.
Great discussion, Susan. Definitely an interesting time as we really get to put our money where our mouths are now!
The high fiving about the good times is just as bad as the panicking about the bad times. People talk about all the money they “lost” from this recent drop, but the reality is that’s only a paper drop until they sell. It’s just as bad as everyone who was bragging about owning Tesla when it hit $900/share a couple months ago but have been silent since then.
Something that gives me perspective is an old 401k from a former employer that I haven’t contributed to for over ten years but never rolled over because it’s with a good financial firm, has low fees, and has access to some top Vanguard funds. Looking at the massive year-to-date drop is a gut punch, but then I looked back at the balance when I left that company ten yers ago and I’m currently still well beyond double the initial contributions. I’m still contributing to my current 401k and, yeah, it feels silly looking back at the past couple of months and seeing my monthly contributions evaporate in a few days, but I know there’s no way I can predict what the market is going to do in the near term and I know these contributions are buying at discount compared to when the market was hitting all time highs.
One thing that affects my attitude is that I live in one the highest property tax states so I can never truly own my home. Tax escrow is currently the single largest component of my monthly mortgage payment and, given the historic rate of increase, it will be greater than principal plus interest combined long before my mortgage is paid off. If it came down to it, my mortgage company will be way easier to work with than the government, so I’d rather have access to assets that I can sell to pay taxes if it came down to it than tying it up paying off a mortgage that’s not so bad relatively speaking. Life keeps me here for now, but someday I will move to a state where owning a home means more and, in that case, I might be more aggressive about eliminating the mortgage.
And I apologize, Sandy, for using the wrong name in my last reply! Need to pay better attention to the details like that.
Has anyone compared the net worth comparing the payoff vs invest after the payoff has occurred, say 5, 10 or 20 years?
Yes, it should be more of a no-brainer that the typical returns from equities would be higher than the mortgage paid and thus your net worth would be greater investing. But, when you pay off the house you now have a much larger shovel to invest with. The P&I plus what you had been adding to the principle is now a significantly larger value that will allow you to invest more dollars at a higher return than if you did the invest only option. You just have to postpone those returns 3-10? years or so before you overtake the crowd that did the invest only. I’ve run some excel net worth comparisons for my situation and it is about at year 10 year when the payoff-then-invest overtakes by the invest-only philosophy. Overall, I really don’t think there is a right or wrong decision here as life changes all the time.
Clay,
its cool to see this progression. On line 37 the cumulative FV is $14,523.85, which is what you would have had if you paid of the mortgage and just invested the payments. Which means with the opportunity cost removed Z37-U37 comparative gain is $31,763.61.
That’s a substantial difference in just a 3 year period. Given the 2020 Market event too, seems like this is by far the more productive method as long as you have the risk tolerance for the up and down.
I wish there was a “value” one could put on the mental anguish such as a person like myself goes through with having a mortgage. Even though I have always had more than enough to pay the mortgage payment plus additional principal.
Mentally, it beats me up pretty bad. As soon as i hit the submit button online, there is another mortgage statement in my mailbox the very next day. It’s like the devil will not get off my shoulders!
That being said. I had 93,000 left on my mortgage when my father passed away a couple of months ago. I have 2 other brothers and we are all getting 3 inheritance payments. Each one will be larger than the last one. The first payment was three thousand shy of paying off the mortgage. I always knew that investing the amount of the mortgage. Would be better in the long run.
However, this is without incorporating the weight, which in my case is substantial, of the mental anguish that the mortgage represents to me. Probably because when I was younger. I did not listen to my father and went way over my head in debt. I came to my senses and finally listened to him. I finally have zero debt. Other than the cable, electric, water, sewer, and property taxes.
Besides the mental weight, my oldest brother, which happens to be the executor of the will. Said I absolutely have to pay the mortgage off as my father was a cosigner and his name is on the deed to the house. I know there other ways to get his name off, but my brother was insistent that I pay off the mortgage to get his name off the deed. With every one still grieving. I did not want to start a family feud. I bit my lip and sent the check off to the mortgage company.
I can tell you the amount of weight lifted off my shoulders. Mentally, is priceless. I am still beating myself up over not investing that 90k.
Now, what was the mortgage payment and extra principal, goes to a nice s&p500 index fund. I no longer have to worry if my home business will make enough to pay the mortgage. Then the next two inheritance payments will go right into the stock market. Albeit, middle of the road, risk wise. Perhaps at 48 years young, I shouldn’t beat myself up so much over sending the check in.
This post is due for an update, now a few years later!
I’d love to see an update with current mortgage interest rates. Would the decision still be similar? Recently purchased our dream home and put 20% down. Interest rate is 6.025% Have 1 paid for home that is currently rented out long term. Should we pay off the mortgage as fast as possible? Or invest any extra? No other debt…and we’ve been debt free since 6/3/2014 until this recent purchase…feels a little icky but I’m not convinced we should pay it off again…